SICP Exercise 2.50: Flipping Painters

Define the transformation flip-horiz, which flips painters horizontally, and transformations that rotate painters counterclockwise by 180 degrees and 270 degrees.

Okay, so first of all here's our default frame: The origin is at (0, 0), edge1 is the horizontal edge, ending at (1,0) and edge2 is the vertical edge, ending at (0, 1). And for comparison with later images, here's what we get when we invoke (wave window): To flip a painter horizontally we need to retain the vertical orientation properly, but invert the horizontal orientation. I.e. we want our coordinates system to be: Here the origin is at (1, 0), edge1 is still the horizontal edge, but goes in the oposite direction and ends at (0,0) and edge2 is still the vertical edge, but is on the right of the frame, ending at (1, 1). This translates directly into the following transformation:

(define (flip-horiz painter)
  (transform-painter painter
                     (make-vect 1.0 0.0)
                     (make-vect 0.0 0.0)
                     (make-vect 1.0 1.0)))

Calling ((flip-horiz wave) window) gives us: Rotate the frame by 180° moves the origin to the opposite corner and pulls the edges around with it: Here the origin is at (1, 1), edge1 is still the horizontal edge, but is at the top of the frame and goes in the oposite direction, ending at (0, 1), and edge2 is still the vertical edge, but is on the right of the frame and is inverted, ending at (1, 0). This gives us the following transformation:

(define (rotate180 painter)
  (transform-painter painter
                     (make-vect 1.0 1.0)
                     (make-vect 0.0 1.0)
                     (make-vect 1.0 0.0)))

Calling ((rotate180 wave) window) gives us: Finally, rotating the frame by 270° gives us the following coordinates system: Here the origin is at (0, 1), edge1 is now the (inverted) vertical edge on the left-hand side, ending at (0, 0), and edge2 is now the horizontal edge at the top, ending at (1, 1). So our final transformation is:

(define (rotate270 painter)
  (transform-painter painter
                     (make-vect 0.0 1.0)
                     (make-vect 0.0 0.0)
                     (make-vect 1.0 1.0)))

Calling ((rotate270 wave) window) gives us:

SICP Exercise 2.49: Primitive Painters

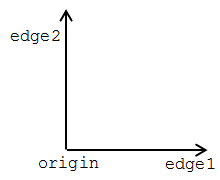
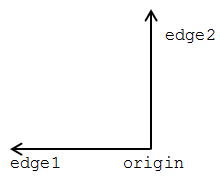
Use segments->painter to define the following primitive painters:

1. The painter that draws the outline of the designated frame.
2. The painter that draws an "X" by connecting opposite corners of the frame.
3. The painter that draws a diamond shape by connecting the midpoints of the sides of the frame.
4. The wave painter.

Before we start defining a load of segments, let's first have a look at the outline, diamond and painters... To draw an outline of the frame we need four segments:

• One from the bottom-left corner to the bottom-right corner
• One from the bottom-right corner to the top-right corner
• One from the top-right corner to the top-left corner
• One from the top-left corner to the bottom-left corner

Similarly we need four segments to draw a diamond shape, except these connect the midpoints of the sides:

• One from the midpoint of the bottom side to the midpoint of the right side
• One from the midpoint of the right side to the midpoint of the top side
• One from the midpoint of the top side to the midpoint of the left side
• One from the midpoint of the left side to the midpoint of the bottom side

Notice how these painters need a connected series of segments. I.e. the end point of one segment becomes the start point of the next segment, and so on throughout the segments. Also note that, although the wave painter's segments don't form a closed polygon, it's made up of five sets of connected segments. If we were to manually create the segment lists for these painters we'd end up with a large number of make-segment chains along the lines of:

  (make-segment (make-vect x1 y1) (make-vect x2 y2))
  (make-segment (make-vect x2 y2) (make-vect x3 y3))
  (make-segment (make-vect x3 y3) (make-vect x4 y4))
  …

Rather than doing this we can produce a helper procedure that will take a list of vectors and produce a connected sequence of segments such that the first segment starts with the first vector and ends with the second vector, the second segments starts with the second vector and ends with the third vector and so on. The resulting list of segments will contain one less segment than there are vectors. To produce this we can have a procedure that takes an arbitrary number of vectors (via the syntax we learned in exercise 2.20), takes the first vector as the starting point and then iterates through the remaining list, producing a segment linking the the current start point with the current list item and moving the start point along to the current list item at each iteration. Here's the implementation I produced to do this:

(define (build-segments-list . vect-list)
  (define (build cur-vect remaining)
    (if (null? remaining)
        nil
        (cons (make-segment cur-vect (car remaining))
              (build (car remaining) (cdr remaining)))))
  (if (null? vect-list)
      nil
      (build (car vect-list) (cdr vect-list))))

Using this we can then define procedures for drawing the outline and diamond slightly more succinctly than would otherwise be possible as:

(define outline
  (segments->painter (build-segments-list (make-vect 0.0 0.0)
                                          (make-vect 0.0 1.0)
                                          (make-vect 1.0 1.0)
                                          (make-vect 1.0 0.0)
                                          (make-vect 0.0 0.0))))

(define diamond
  (segments->painter (build-segments-list (make-vect 0.0 0.5)
                                          (make-vect 0.5 1.0)
                                          (make-vect 1.0 0.5)
                                          (make-vect 0.5 0.0)
                                          (make-vect 0.0 0.5))))

To make the results of these easier to see I produced a procedure, quad that draws a 2 × 2 grid, with each cell containing the requested painter:

(define (quad painter)
  (let ((side-by-side (beside painter painter)))
    (below side-by-side side-by-side)))

Then I can use:

((quad outline) window)

...to produce:
...and...

((quad diamond) window)

...to produce:
We can't use build-segments-list for drawing an "X", however. There is no connected series of segments here. Instead we need to produce two segments that join the diagonally opposite corners:

(define draw-x
  (segments->painter (list (make-segment (make-vect 0.0 0.0) (make-vect 1.0 1.0))
                           (make-segment (make-vect 0.0 1.0) (make-vect 1.0 0.0)))))

Here:

((quad draw-x) window)

...gives:
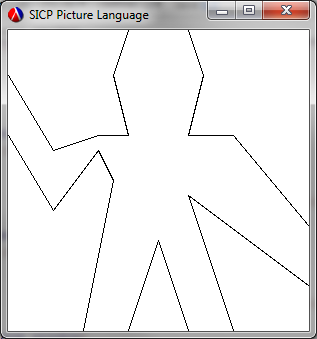
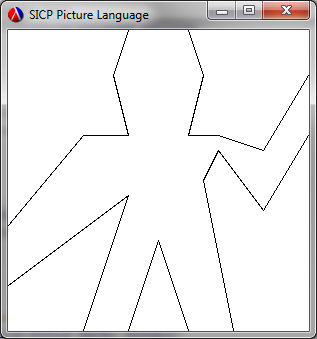
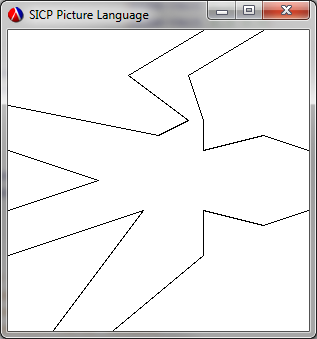
Finally we can address wave. Now there doesn't appear to be a handy set of coordinates kicking around for this, so I resorted to my paper copy of the book and a ruler. But, as noted above, this has five sets of connected segments, so we can use build-segments-list again to simplify the procedure slightly. Note that, as each build-segments-list call produces a list of segments we have to append them together in order that we can then pass them through to segments->painter:

(define wave
 (segments->painter
   (append (build-segments-list (make-vect 0.0  0.85)
                                (make-vect 0.15 0.6)
                                (make-vect 0.3  0.65)
                                (make-vect 0.4  0.65)
                                (make-vect 0.35 0.85)
                                (make-vect 0.4  1.0))
           (build-segments-list (make-vect 0.6  1.0)
                                (make-vect 0.65 0.85)
                                (make-vect 0.6  0.65)
                                (make-vect 0.75 0.65)
                                (make-vect 1.0  0.35))
           (build-segments-list (make-vect 1.0  0.15)
                                (make-vect 0.6  0.45)
                                (make-vect 0.75 0.0))
           (build-segments-list (make-vect 0.6  0.0)
                                (make-vect 0.5  0.3)
                                (make-vect 0.4  0.0))
           (build-segments-list (make-vect 0.25 0.0)
                                (make-vect 0.35 0.5)
                                (make-vect 0.3  0.6)
                                (make-vect 0.15 0.4)
                                (make-vect 0.0  0.65)))))

Then we can test it out, using:

((quad wave) window)

...to produce:

SICP Exercise 2.48: Segments

A directed line segment in the plane can be represented as a pair of vectors -- the vector running from the origin to the start-point of the segment, and the vector running from the origin to the end-point of the segment. Use your vector representation from exercise 2.46 to define a representation for segments with a constructor make-segment and selectors start-segment and end-segment.

As with the representation we produced for vectors in exercise 2.46, segments lend themselves naturally to being represented as pairs. We can put the start of the segment in the first element of the pair, and the end of the segment in the second element of the pair. Then we can access the start and end using car and cdr respectively:

(define (make-segment start-v end-v)
  (cons start-v end-v))

(define (start-segment seg)
  (car seg))

(define (end-segment seg)
  (cdr seg))

This then allows us to represent segments and access their components:

> (define segment (make-segment (make-vect 10 5) (make-vect 30 40)))
> segment
'((10 . 5) 30 . 40)
> (start-segment segment)
'(10 . 5)
> (end-segment segment)
'(30 . 40)