The "eight-queens puzzle" asks how to place eight queens on a chessboard so that no queen is in check from any other (i.e., no two queens are in the same row, column, or diagonal). One possible solution is shown [below]. One way to solve the puzzle is to work across the board, placing a queen in each column. Once we have placed k - 1 queens, we must place the kth queen in a position where it does not check any of the queens already on the board. We can formulate this approach recursively: Assume that we have already generated the sequence of all possible ways to place k - 1 queens in the first k - 1 columns of the board. For each of these ways, generate an extended set of positions by placing a queen in each row of the kth column. Now filter these, keeping only the positions for which the queen in the kth column is safe with respect to the other queens. This produces the sequence of all ways to place k queens in the first k columns. By continuing this process, we will produce not only one solution, but all solutions to the puzzle.
We implement this solution as a procedure queens, which returns a sequence of all solutions to the problem of placing n queens on an n × n chessboard. Queens has an internal procedure queen-cols that returns the sequence of all ways to place queens in the first k columns of the board.
(define (queens board-size)
(define (queen-cols k)
(if (= k 0)
(list empty-board)
(filter
(lambda (positions) (safe? k positions))
(flatmap
(lambda (rest-of-queens)
(map (lambda (new-row)
(adjoin-position new-row k rest-of-queens))
(enumerate-interval 1 board-size)))
(queen-cols (- k 1))))))
(queen-cols board-size))
In this procedure rest-of-queens is a way to place k - 1 queens in the first k - 1 columns, and new-row is a proposed row in which to place the queen for the kth column. Complete the program by implementing the representation for sets of board positions, including the procedure adjoin-position, which adjoins a new row-column position to a set of positions, and empty-board, which represents an empty set of positions. You must also write the procedure safe?, which determines for a set of positions, whether the queen in the kth column is safe with respect to the others. (Note that we need only check whether the new queen is safe -- the other queens are already guaranteed safe with respect to each other.)
So what will our representation for board positions be? Well, as we only have one type of piece on the board, the queen, we don't need to concern ourselves with recording which type of piece we're putting in each position. We only need to record the row and position of each placed piece, so a pair will do nicely for this. As for representing a set of board positions, we can represent this as a list of such pairs. That means that
empty-board will just be an empty list and
adjoin-position will just
cons a pair representing the position of the placed piece onto the list representing the set of board positions so far:
(define empty-board nil)
(define (adjoin-position row column board)
(cons (cons row column) board))
Let's give ourselves a couple of selectors as well for extracting the row and column from a given position:
(define (get-row position)
(car position))
(define (get-column position)
(cdr position))
That's the easy bit done. We need to write
safe? now. As stated in the exercise, a position is safe if there are
no two queens are in the same row, column, or diagonal. Now
safe? is called with the column number,
k, and the set of
positions to be validated. We know that the positions of the queens in the first
k - 1 columns have already been validated as safe - we just need to validate that the newly added queen position is also safe. So before we can even check the positions we need to find the queen that's just been added and also produce the set of positions we need to validate (i.e. all but the newly added queen). Both of these involve filtering the list of
positions... In the former case we want to filter to just those queens in the column we've added. There should one and only be one of these, so let's assume that and extract it from the filtered list using
car. For the latter case, assuming we've already found the first queen in the column we've just added, we can just filter the list to remove any queens in that position. Here's a couple of procedures that will do this for us:
(define (get-first-in-column column positions)
(car (filter (lambda (position)
(= (get-column position) column))
positions)))
(define (filter-out-position filter-position positions)
(let ((row (get-row filter-position))
(column (get-column filter-position)))
(filter (lambda (position)
(not (and (= (get-row position) row)
(= (get-column position) column))))
positions)))
Now onto the actual checking itself. To check whether or not a newly-added queen in a particular row and column is a safe position we need to compare it with all the other queen positions and, for each one, confirm that it's not in the same row or column and that it's not on a diagonal. The first two tests here are easy. The second one's a little bit tricky, but easy enough if you note that the diagonal positions that are
n columns away from a particular position are also
n rows away from that position. I.e. if we've got a piece in row 4, column 5, then the positions that are diagonal to this in column 2 are 3 columns away, and so are 3 rows away to: in rows 1 and 7 (i.e. 4 - 3 and 4 + 3 rows away). Also note that we don't need to worry if this takes us outside the board size - there shouldn't be any pieces there anyway! Anyway, here's a test to check whether a newly added queen in (
row,
column) is safe with respect to another queen in (
other-row,
other-column):
(define (is-safe-position? row column other-row other-column)
(let ((other-column-diff (- column other-column)))
(and (not (= row other-row))
(not (= column other-column))
(not (= (+ row other-column-diff) other-row))
(not (= (- row other-column-diff) other-row)))))
Finally we can put this all together. We just need to extract the position of the queen we've just added, get the list of other queens' positions, and then iterate across those positions and check each one is safe with respect to the newly-added queen (via
is-safe-position?). We can do this iterative step using
accumulate. A newly added queen is safe if it's safe with respect to the first queen in the list of positions
and with respect to the second
and with respect to the third, and so on. So if we assume that the queen position is safe to begin with (i.e.
initial is
#t) then we can determine whether the position's safe by
anding the accumulated result so far with the results of testing the next position in the list with
is-safe-position?. Of course that's easier to express in code than words:
(define (safe? column positions)
(let ((test-position (get-first-in-column column positions)))
(let ((row (get-row test-position))
(column (get-column test-position))
(other-positions (filter-out-position test-position positions)))
(accumulate (lambda (position preceding-positions-safe)
(and (is-safe-position? row
column
(get-row position)
(get-column position))
preceding-positions-safe))
#t
other-positions))))
Now we can put this to the test:
> (queens 0)
'(())
> (queens 1)
'(((1 . 1)))
> (queens 2)
'()
> (queens 3)
'()
> (queens 4)
'(((3 . 4) (1 . 3) (4 . 2) (2 . 1)) ((2 . 4) (4 . 3) (1 . 2) (3 . 1)))
> (queens 5)
'(((4 . 5) (2 . 4) (5 . 3) (3 . 2) (1 . 1))
((3 . 5) (5 . 4) (2 . 3) (4 . 2) (1 . 1))
((5 . 5) (3 . 4) (1 . 3) (4 . 2) (2 . 1))
((4 . 5) (1 . 4) (3 . 3) (5 . 2) (2 . 1))
((5 . 5) (2 . 4) (4 . 3) (1 . 2) (3 . 1))
((1 . 5) (4 . 4) (2 . 3) (5 . 2) (3 . 1))
((2 . 5) (5 . 4) (3 . 3) (1 . 2) (4 . 1))
((1 . 5) (3 . 4) (5 . 3) (2 . 2) (4 . 1))
((3 . 5) (1 . 4) (4 . 3) (2 . 2) (5 . 1))
((2 . 5) (4 . 4) (1 . 3) (3 . 2) (5 . 1)))
> (queens 6)
'(((5 . 6) (3 . 5) (1 . 4) (6 . 3) (4 . 2) (2 . 1))
((4 . 6) (1 . 5) (5 . 4) (2 . 3) (6 . 2) (3 . 1))
((3 . 6) (6 . 5) (2 . 4) (5 . 3) (1 . 2) (4 . 1))
((2 . 6) (4 . 5) (6 . 4) (1 . 3) (3 . 2) (5 . 1)))












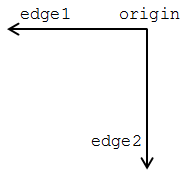

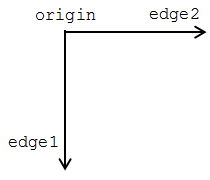









 Now with that done we can actually get on to the exercises themselves.
Now with that done we can actually get on to the exercises themselves.